Let’s fix this old question of mine:
What patterns are there in these quadrilaterals: rhombus, parallelogram, trapezoid, rectangle, and square?
Like so many of my Depth and Complexity questions, this is not actually deep or complex! I’m just asking for a list. And my students can simply write, “These quadrilaterals all have four sides and four angles.” And that’s it.
So let’s set up a sequence of questions, rather than a low-level, one-off. And I’m going to frame it around the universal theme of conflict.
Introduce The Big Idea
I’d begin with a funny story about a conflict between my wife and I over some small detail. Then we could discuss details that cause conflict between characters, conflict on the playground, or famous historical conflicts.
After that, we’ll move on and ask students to spot the details that might cause conflict between quadrilaterals. So we’re really using a big idea of 🏛️ “Details can lead to conflict.”
You: Class, what details would cause these shapes to have conflict?
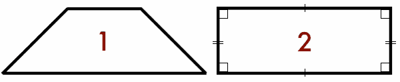
With well-chosen images, students will jump on this idea quickly.
Student: Shape 1 starts to go up to a point, but 2 has only straight sides.
Increase Expectations
We can gradually increase our expectations, sneaking academic vocabulary in as it becomes useful (rather than dumping a bunch of out-of-context vocab at the beginning of the lesson).
You: Yes! Those straight sides are called parallel lines! This means…
I write down the student’s idea along with the academic language. Put the 👄 lips next to it if you’re using Depth and Complexity.
Keep going, using new shapes. Deliberately plan these image combinations to draw out certain details. A rectangle next to a parallelogram highlights different details than a parallelogram and a rhombus.
Students might name details that don’t match your expectations, like “one is bigger than the other.” Don’t dismiss those ideas. Write them down. But, as you move through the lesson, prune those options away until you’re down to the desired set.
You, eventually: We came up with tons of details that cause conflict, some I hadn’t even thought of! Let’s focus on these three details as we move towards the quadrilateral battle!
What if…
Q: I carefully and deliberately planned my shape images to highlight the conflicts, but no one thought of congruent sides!
A: Then just tell them. “Hey, there’s one more I noticed. Look at this shape’s sides. They’re exactly the same size! I bet there’d be conflict because the other shape has no sides that are the same. When sides are the same size we call them congruent.”
Drawing New Recruits
We’ve got the required details. Now let’s check students’ understanding. Ask them to draw “quadrilateral recruits” based on your requirements.
You: A quadrilateral army is recruiting shapes with two sets of parallel lines. Nothing else matters, but they want a wide variety. Create three recruits on your whiteboards.
Check their drawings. Adjust your lesson as necessary. Kids might draw faces on their quadrilaterals. That’s awesome.
What an interesting group of shapes! Yet they all fit the requirements. These recruits are called parallelograms!
Encourage students to explore a wide variety of shapes that fit the requirements. Check if anyone drew a rectangle. Confirm that, yes indeed, a rectangle is a type of parallelogram.
Another army wants shapes with two pairs of parallel lines and four right angles. Create three different recruits.
Check their drawings.
Great! I see lots of different versions of this shape: the rectangle.
Did anyone draw a square? Point out that this is a type of rectangle as well.
Ranking Conflict
Now your class will more formally identify conflicts between quadrilateral. Put students in groups. Grab those students who you noticed struggling and work directly with them.
Students work together to fill out a conflict table:
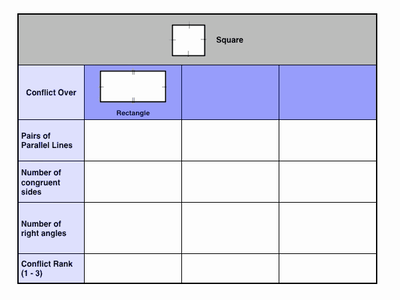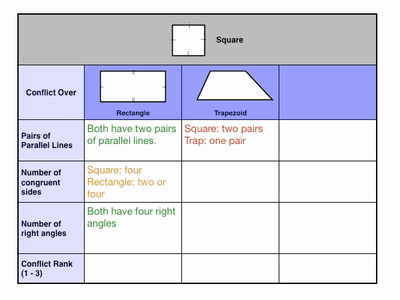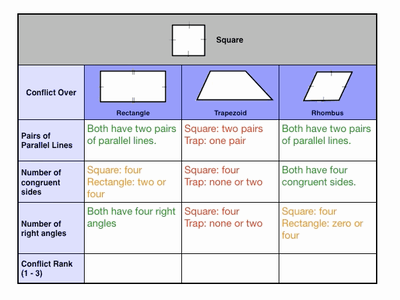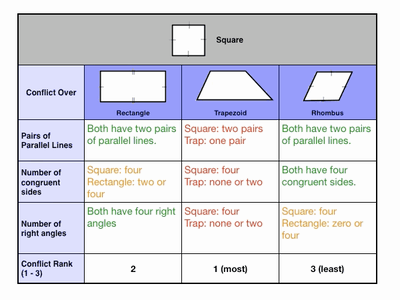
Notice that we hit the high-level thinking skill of “judgment” by asking kids to rank shapes by conflict. This leads to debate, and when students debate about quadrilaterals, it’s a great day.
The academic vocabulary is fully integrated now, but we got here slowly by setting the stage with “conflict.”
The Final Challenge
This 3rd-grade common core standard wants students to “draw examples of quadrilaterals that do not belong to any of these subcategories.” What a great final step!
Students! There is a mutant quadrilateral on the loose. It fits into no known categories but still has four sides. What could it look like?
And finally, this lesson sets up a great math narrative. Feel free to integrate a skit, comic book, or short story about The Great Quadrilateral Conflict!

