Mathematical Curiosities

Sometimes you encounter that math student who is simply intrigued by strange numbers. Here are some famous (and not so famous) sets of numbers that have curious properties.

The Fibonacci Series

The Fibonacci series starts with zero and one. To find the next number, and add the previous two numbers together:

0 + 1 = 1
1 + 1 = 2
1 + 2 = 3
2 + 3 = 5

0, 1, 1, 2, 3, 5, 8, 13…

The Fibonacci series has many interesting appearances in nature and is related to our next curiosity: the golden ratio.

The Golden Ratio

Known as phi or φ, the golden ratio is approximately 1.618.

A golden rectangle is a rectangle whose sides have a ratio of φ. Continuing to divide this rectangle by the golden ratio leads to some amazing visual properties:

Rect

Note that if you divide a Fibonacci number by its predecessor, you always hover around the golden ratio. And the farther you go in the sequence, the closer to the golden ratio you get:

5 ÷ 3 = 1.667
8 ÷ 5 = 1.6
13 ÷ 8 = 1.625
21 ÷ 13 = 1.615

Images that make use of the golden ratio are considered to be pleasing to the human eye. Dali’s The Sacrament of the Last Supper is purposefully based around the golden ratio, and many other works of art incorporate the rectangle (although perhaps accidentally!).

Perfect Numbers

A perfect number’s factors sum to the number itself:

6 = 1 + 2 + 3
28 = 1 + 2 + 4 + 7 + 14
496 = 1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248

These get large pretty quickly! Here is far more information on the perfect numbers.

Pythagorean Triples

A Pythagorean Triple consist of three whole numbers that satisfy the equation a² + b² = c², also known as the Pythagorean theorem.

Here are the first three triples:

3 + 4 = 5 (9 + 16 = 25)
5 + 12 = 13 (25 + 144 = 169)
7 + 24 = 25 (49 + 576 = 625)

Figurate Numbers

Figurate numbers look like the shape that they are named after. There are tons of these, but we’ll examine just three.

Perfect Squares

These numbers can be arranged to look like squares: 4,9,16

Squares

The enemy of a perfect square is a square-free number: one who is divisible by no perfect squares.

1, 2, 3, 5, 6, 7, 10, 11, 13…

Note that 8 doesn’t make the cut since it’s divisible by 4, 9 is divisible by 9, and 12 is divisible by 4.

Triangular Numbers

These numbers can be arranged into a stacked triangle: 3, 6, 10, 15, 21

Triangles

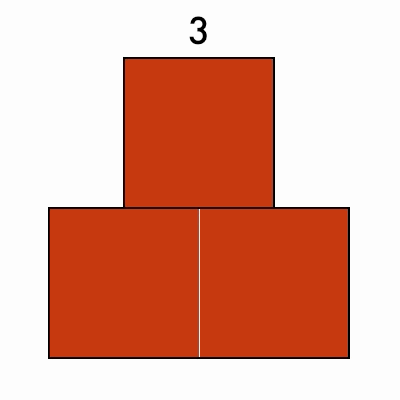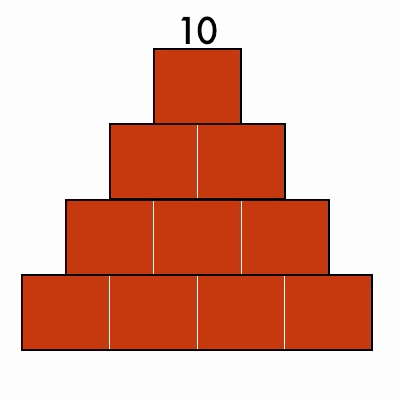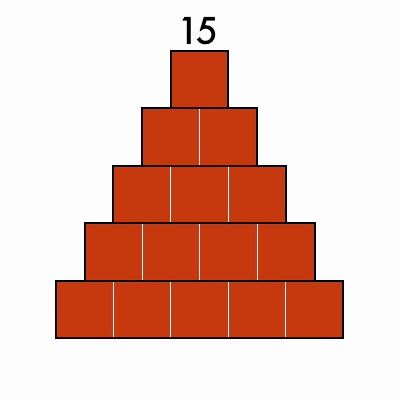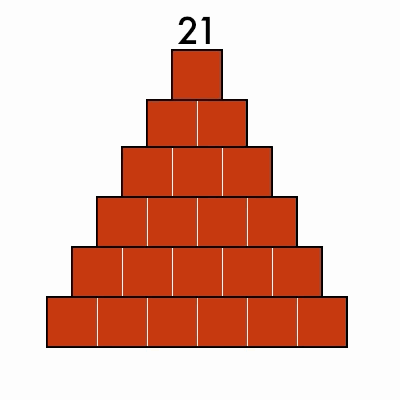
Bonus: can you find numbers that are both triangular and perfect squares?

Centered Hexagonal Numbers

These numbers can be arranged into a hexagon, starting with one point in the middle:

1, 7, 19, 37

Hex