If you were a kid like me, you loved Sesame Street’s “not like the others” videos. But you especially delighted in finding the non-obvious answers.
Sure, the blue balloon is obviously the outlier. But here’s why each of the others also stands out…
I’m sure you have students who think the same way. In fact, this kind of contrarian thinking will be pretty common with your most curious and creative minds. Some kids want to find the unexpected answer.
Lean Into Ambiguity
So, let’s purposefully set up tasks that lean into this kind of thinking.
Rather than giving students four choices where one is right, we’ll give four choices where none are right – and none are wrong. This moves students’ focus from “Am I right?” to “Let me explain my cool thinking!!!”
Now, a few of your students will take to these tasks immediately, but if you want to encourage interesting thinking from more of your class, it pays to set things up well. So, here are some realizations I’ve had while developing a whole bunch of tasks using this framework.
Tip 1: Remove Obvious Answers
If I ask my students “Which country is not like the others?” and offer these four choices, I’m going to have a problem. Do you see it?
- China
- South Korea
- Guatemala
- Japan
Three options are in Asia and one is from across the globe. I’ve created such an obvious outlier that some students won’t see past it. Guatemala like a bright light shining in their faces.
So, instead, consider which of these countries is not like the others:
- Canada
- The United States
- England
- Australia
By removing an obvious option, we’ll get more students thinking in interesting ways. Perhaps England doesn’t belong because all of the other countries were once under its control. Or maybe it’s Australia because it’s the only one in the southern hemisphere. Is it Canada, because it’s the only country with an officially French-speaking region?
You’ll see students start looking each country up, digging for facts that make each option unique.
Tip 2: Call Out The Kind of Answers You Don’t Want
Do you want students to say something like, “The United States doesn’t fit because its name has three words”? If not, then call it out in the beginning. Say, “Now, let’s not give surface-level answers that are about the countries’ names. Let’s dig deeper into information about the countries themselves.”
I personally don’t like reasons that are just “biggest” or “smallest” (or most populous, least landmass, greatest GDP, etc), since those are not really “unique” to the country. In any set of countries, one will always be the biggest and one will always be the smallest. So I’d just tell students up front:
Rather than saying, “County X is the bigget/northernmost/etc,” begin your reasons with, “Country X is the only one in this group that…”
This keeps them focused on uniqueness.
Now, you might have no problem with these kinds of answers! You do you. But it helps to be up front with your expectations.
Tip 3: Encourage Multiple Reasons
Eventually, students will start finding multiple reasons why each choices is different from the other three. Can they find two reasons for each country? Three!?
But, they don’t have to force it! Some options may have five reasons and some may have just one. That’s fine! We want students to be flexible in their thinking.
You may also find that some students come in on Monday, excited to show you another idea they came up with for Australia. Isn’t that the best!?
Tip 4: A Warning About Visuals
If you do this with countries, beware showing the countries’ flags. It’s hard for kids to ignore the visual differences in the symbols. Consider the low-level responses that the example below would generate:
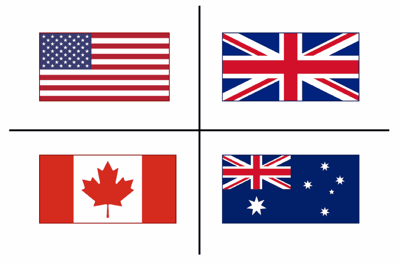
Students will be so tempted to say, “Canada is not like the others because its flag doesn’t have blue (or it is the only one with a leaf or it doesn’t have a star).” That’s not the level of thinking I want, so I’d be sure to mention that up front. “Class, we’re not merely describing the flags. We’re thinking about the actual countries.”
If you show four types of animals, make sure to tell students, “I don’t want you to tell me the differences in the pictures. Instead, tell me how the animals themselves are different.”
An Example
Which of these planets is not like the others?
- Mercury
- Saturn
- Uranus
- Mars
Notice that I’ve avoided using earth, since it’s too obvious of an outlier. I’ve chosen two inner planets and two outer planets. I made sure that Saturn wasn’t the only planet with rings. I picked examples to help students to find interesting, not obvious, reasons for each planet.
Now, if a kid says, “Mars is the only one that’s red,” I’m not going to make a big deal about it. I’ll just say, “Nice! Write it down. Now, what else can you find?”
Self-Differentiating
These tasks are a great example of low ceiling and high floor. They are easy for students to have immediate success. Everyone can get a quick win. But these tasks also allow for your top notch geniuses to keep going and going (and going!). Great tasks allow for multiple levels of students to have success. You don’t need three different versions for your three different groups.
Try It With All Kinds Of Content
You can set Not Like Thoe Other tasks up across all content areas. You could use:
- types of animals
- characters from a novel
- stories from one author
- pieces of art
- battles from The American Civil War
- biomes
- elements from the period table
- If you’re working with math, you’re going to love Which One Doesn’t Belong?
Over at Byrdseed.TV, I’m building out ideas across other disciplines with some extra help from my friend Mike Saltz. (Yes, he came up with Microstate of Europe.)