It’s my mission in life to make sure students are thinking rather than merely remembering when they’re at school. Here are a bunch of ideas and resources for promoting thinking in math.
I like to say that these kinds of tasks and resources are proud of math. They don’t try to hide math behind a game. They show that math is inherently interesting.
Table of Contents
- How Did We Get Here?
- Not Like The Others
- What’s The Question
- Guess My Number
- Open Middle
- Visual Patterns
- Would You Rather…
Required Reading
If you haven’t read these articles yet, they’ll provide background for the why behind these ideas.
1. How Did We Get Here?
This could be a daily warmup. To add complexity, we begin at the end and ask students to come up with multiple paths that could have led us there.
For example, write a big “17” on the board and ask your students “Come up with ten, no twenty, no fifty ways we could get to 17?”
Some simple paths include:
- 16 + 1
- 10 + 7
- 20 – 3
These are great starting points but include some constraints to force students to explore even more creative ways to arrive at 17:
- You must take exactly three steps (10 + 3 + 4, 8 × 2 – 1)
- You must use a decimal (34 × 0.5)
- You must incorporate a square root (√81 × 2 – 1)
There are literally an infinite number of ways to arrive at this one number, and this task encourages students to use their different math tools. Start each day with a new number. Try fractions, decimals, and negative numbers.
This works with all ages because we can ask students to use grade-level concepts. Primary students might just add and subtract. Upper elementary might include fractions or division.
This task is complex, not merely difficult. It has a high ceiling.
2. Not Like The Others
A common math problem is to ask students to identify a pattern, given:
3, 6, 9, 12
But, using the same set of numbers, we can ask a different question: Which number is not like the others?
Of course, there is no “right” answer. 12 might be the most obvious outlier because it is two-digits, but students might say:
- 3 is the only prime
- 9 is the only perfect square
- We can double 3 to get 6 and double 6 to get 12, but 9 doesn’t fit this pattern
Again, students with more math tools will be able to come up with more reasons to rule out certain numbers.
Update: Mary Bourassa has created a huge resource of samples that she calls Which One Doesn’t Belong?
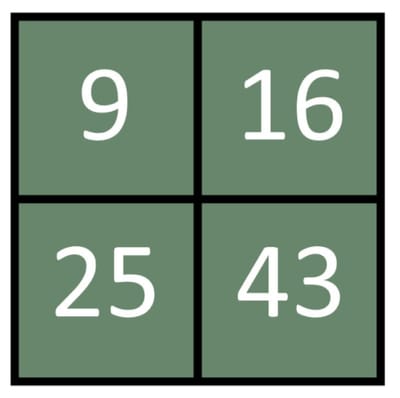
I also have developed a bunch of “Not Like The Others” videos at Byrdseed.TV.
3. What’s the Question?
Inspired by Dan Meyer, show an intriguing image and ask your students, “What question could we ask?” Make sure to tell them they don’t have to solve it or they’ll be afraid to ask any difficult questions!
For example, show this image of a packed stadium.
What question could we ask, even if we don’t know how to answer it yet?

Possible questions include;
- how many people are at the stadium
- how much did people spend on tickets
- how many hot dogs were sold at this game
4. Guess My Number
As a variation on “20 Questions,” allow the class to ask a certain number of questions to determine the number that’s “in your head.”
Questions might include:
- Is it odd or even?
- Positive or negative?
- Integer or non-integer?
- Rational or irrational?
- Greater than 10 or less than 10?
Of course, once they get the idea, students can choose their own numbers and work within groups to practice together, or make you guess their number.
5. Open Middle
Open Middle comes from my real-life pal Robert Kaplinsky (among others).
This order of operations example is a favorite of mine. Using the numbers 0-9 (only one time per number), make the largest number possible:
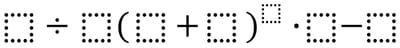
Head over to OpenMiddle.com to see a hint and the solution.
6. Visual Patterns
Fawn Nguyen (and company) have put together a delightful resource for noting and generalizing patterns called Visual Patterns. In each case, the first few iterations of a pattern are shown and then students must determine the 43rd iteration. Here’s one example (from Matt Vaudrey):
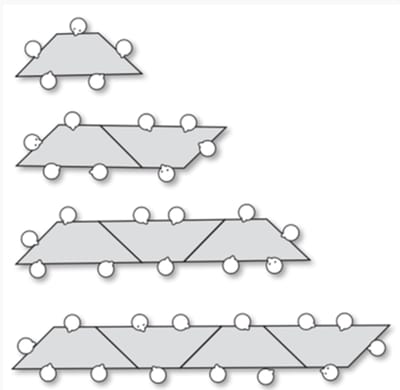
How many seats would there be with 43 tables?
Hit up VisualPatterns.org to see the solution, as well as over 200 other patterns. I’ve also created scaffolded videos in the same vein over at Byrdseed.TV.
7. Would You Rather?
John Stevens shares situations that ask students to wonder which is better? Whether they’re picking a credit card or deciding which circumstances lead to more money, kids have to justify their thinking with their math skills. Check out Would You Rather?
Have a favorite resource to make sure kids are thinking, not merely remembering in math? Send it my way: ian@byrdseed.com.
